LaTeX - um poderoso diagramador de textos (parte 1)
Mostraremos aqui como usar o LaTeX, um editor de texto altamente personalizável e com grande qualidade gráfica.
[ Hits: 63.042 ]
Por: N M S em 12/06/2006
Exemplo
Salve os dados abaixo num arquivo exemplo2.tex e repita o processo de compilação.
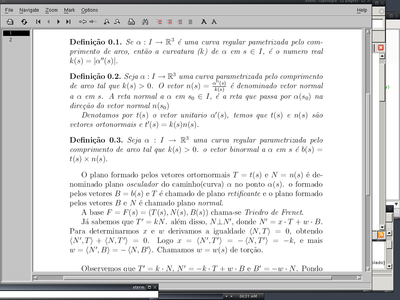
Seu arquivo deve ter exatamente essa aparência:
\documentclass[a4paper,12pt]{article}
\usepackage[brazil]{babel}
\usepackage[latin1]{inputenc}
\usepackage{amsthm,amsfonts}
%
\newtheorem{thm}{Teorema}[section]
\newtheorem{cor}[subsection]{Corolário}
\newtheorem{lem}[thm]{Lema}
\newtheorem{prop}[thm]{Proposição}
%\theoremstyle{definição}
\newtheorem{defn}[thm]{Definição}
% MATH -------------------------------------------------------------------
\newcommand{\Real}{\mathbb R}
\newcommand{\RPlus}{\Real^{+}}
\newcommand{\norm}[1]{\left\Vert#1\right\Vert}
\newcommand{\abs}[1]{\left\vert#1\right\vert}
\newcommand{\set}[1]{\left\{#1\right\}}
\newcommand{\seq}[1]{\left<#1\right>}
\newcommand{\coc}[1]{\left(#1\right)}
\newcommand{\eps}{\varepsilon}
\newcommand{\To}{\longrightarrow}
\newcommand{\BX}{\mathbf{B}(X)}
\newcommand{\A}{\mathcal{A}}
\newcommand{\M}{\mathcal{M}}
\newcommand{\N}{\mathcal{N}}
\newcommand{\Lom}{\mathcal{L}}
\newcommand{\Comp}{\mathcal{K}}
\newcommand{\Basis}{\mathcal{B}}
\newcommand{\anti}{\backslash}
\newcommand{\x}{\times}
\newcommand{\pont}{\cdot}
\newcommand{\implica}{\Rightarrow}
\newcommand{\volta}{\Leftarrow}
\newcommand{\emm}{\rightarrow}
\newcommand{\cb}{\mathcal{B}(X,\Real)}
\newcommand{\bolaa}[1]{\mathbf{B}(#1)}
\newcommand{\bolaf}[1]{\mathbf{B}[#1]}
%%% -----------------------------------------------
\begin{document}
%--------------------------------------------------
\begin{center}
Instituto de Ciências Exatas\\
Departamento de Matemática\\
Geometria Diferencial\\
nfermat\\
\end{center}
\begin{center}
O Triedo de Frenet
\end{center}
\begin{defn}
Se $\alpha:I \emm \Real^3$ é uma curva regular
parametrizada pelo comprimento de arco, então a curvatura
($k$) de $\alpha$ em $s \in I$, é o número real $k(s) = |\alpha''(s)|$.
\end{defn}
\begin{defn}
Seja $\alpha :I \emm \Real^3$ uma curva parametrizada
pelo comprimento de arco tal que $k(s) >0$. O vetor $ n(s) =
\frac{\alpha''(s)}{k(s)} $ é denominado vetor normal a $\alpha$ em $s$.
A reta normal a $\alpha$ em $s_0 \in I$, é a reta que passa por $\alpha(s_0)$
na direção do vetor normal $n(s_0)$\\
\indent Denotamos por $t(s)$ o vetor unitário $\alpha'(s)$,
temos que $t(s)$ e $n(s)$ são vetores ortonormais e
$t'(s) = k(s)n(s).$
\end{defn}
\begin{defn}
Seja $\alpha :I\emm \Real^3$ uma curva regular parametrizada
pelo comprimento de arco tal que $k(s) > 0$. o vetor
\textit{binormal} a $\alpha$ em $s$ é $b(s) = t(s)\x n(s)$.
\end{defn}
\indent O plano formado pelos vetores ortornormais $T=t(s)$
e $N=n(s)$ é denominado plano \textit{osculador} do caminho(curva) $\alpha$
no ponto $\alpha(s)$.
o formado pelos vetores $B=b(s)$ e $T$ é chamado
de plano \textit{retificante} e o plano formado pelos vetores
$B$ e $N$ é chamado plano \textit{normal}.\\
\indent A base $F=F(s)=(T(s),N(s),B(s))$ chama-se \textit{Triedro de Frenet}.
\\
\indent Já sabemos que $T'=kN$. além disso, $N\bot N'$, donde $N'=
x\pont T + w\pont B$. Para determinarmos $x$ e $w$ derivamos a igualdade
$\seq{N,T}=0$, obtendo $\seq{N',T} + \seq{N,T'} = 0$.
Logo $x=\seq{N',T'}=-\seq{N,T'}=-k$,
e mais $w=\seq{N',B}=-\seq{N,B'}$. Chamamos $w=w(s)$ de torção.\\\\
\indent Observemos que $T'= k\pont N$, $N'=-k\pont T + w\pont B$
e $B'= -w\pont N$. Pondo $F'=(T',N',B')$, temos $F'= A\pont F$,
onde $A$ é uma matriz anti-simétrica definida como:\\
\[ A= \coc{
\begin{array}{ccc}
0 & k & 0 \\
-k & 0 & w \\
0 & -w & 0
\end{array}
}
\]
\textbf{ Aplicações:}\\\\
\begin{thm}
Seja $\alpha :I \emm \Real^3$ uma curva regular, de curvatura não nula.
Então $\alpha$ é planar se, e somente se, $w=0$.
\end{thm}
\begin{proof}
$\volta)$Seja $w=0$, logo $B'=-w\pont N = 0 \implica B$ é constante
$\implica \frac{d}{ds}\seq{\alpha(s)-\alpha(a),B} = \seq{T,B} = 0
\implica \seq{\alpha(s) - \alpha(a),B}$ é constante.
Para $s=a$ temos que $\seq{\alpha(a)-\alpha(a),B} = 0$ logo $\forall s,
\, \seq{\alpha(s)-\alpha(a),B}=0$, ou seja $\alpha(s)$ é planar.\\
$\implica)$
Seja $v$ um vetor ortogonal ao plano que contem $\alpha(s)$.
Logo $\seq{\alpha(s) -\alpha(a),v}=0$. Derivando temos que
$\seq{\alpha'(s),v}=0$ e mais $\seq{\alpha''(s),v}=0$
portanto $\seq{T,v}=0$ e $k(s)\seq{N,v}=0.$
Assim $v \parallel B$ pois como $k(s) \neq 0$, $v\bot N$ e $v\bot T$.
Desse modo $\seq{N,B}=0$ logo $w=\seq{N',B}=0$
\end{proof}
\begin{thm}
Seja $\alpha : I\emm\Real^3$ uma curva regular. Então o traço
de $\alpha$ está contido numa circunferência de raio
$r>0$ se, e somente se, $w=0$ e $k = \frac 1a.$
\end{thm}
\begin{proof}
\end{proof}
\begin{defn}
Uma curva regular $\alpha:I\emm\Real^3$ é uma \textbf{hélice}, se
existe um vetor unitário $v$ que forma um ângulo constante
com $\alpha'(t),\, \forall t \in I$, isto é,
$\frac{\seq{\alpha'(t),v}}{|\alpha'(t)|}$ é constante.
\end{defn}
\begin{thm}
Seja $\alpha:I\emm\Real^3$ uma curva regular de curvatura e torção
não nulas. Então $\alpha$ é uma hélice se, e somente se, $\frac kw$
é constante
\end{thm}
\begin{proof}
\end{proof}
%----------------------------------------------------
\end{document}
% ---------------------------------------------------
2. Criando o primeiro documento
3. Pacotes essenciais
4. Exemplo
5. Finalizando
LaTeX, um poderoso diagramador de textos (parte 2)
GmailFS - sua conta de e-mail como um sistema de arquivos no Slackware 10.2
Com software livre você tem e você pode!
Raspberry Pi 4B Como Servidor Linux de Baixo Custo
Técnicas de memorização para facilitar o uso VI (Comandos básicos)
Utilizando o CUPS com estações Windows XP
FwLogWatch - Analisando Registros do IPtables
Não querendo descurar o artigo que fizeste, LateX é um sistema de processamento de texto, não um editor, como diz o título. Editor é o Kile.
Uso LaTeX há alguns anos (no meu curso Universitário é usado para fazer relatórios) e recomendo a conhecida "Uma não tão pequena introdução ao LaTeX2", traduzido do original alemão por um professor meu.
http://alfarrabio.di.uminho.pt/~albie/lshort/
É só sacar o "ptlshort.pdf" para o livro referido ou ainda a "presentation.pdf" que é um resumo ainda maior (apresentação que o professor fez ao alunos sobre o LaTeX2).
Espero que ajude.
Poderia mostrar exemplos mais simples, na minha opinião, e variar um pouco. Apesar de mostrar como fazer um documento estupendo, cheio de formulas matematicas, é interessante mostrar como fazer uma tabela, incluir uma figura. Outra coisa é frizar que o dvi pode ser transformado em postscript ou pdf usando os comandos adequados. Poderia ser um bom artigo.
Acrescento o link para o wiki do grupo Tex-BR com muita informação sobre o LaTeX
http://www.tex-br.org/index.php/P%C3%A1gina_principal
e esse documento de introdução ao LaTeX em português (não é baseado no Kile mas a parte de LaTeX serve)
http://www.mat.ufmg.br/~regi/topicos/intlat.html
Boa noite,
O Latex é genial! Construído sobre o Tex de Knuth, diminui a curva de aprendizado.
E não custa citar o livro do criador do Latex, Leslie Lamport
http://www.amazon.com/gp/product/0201529831/qid=1150163482/sr=1-1/ref=sr_1_1/002-1557260-9688064?s=b...
Bom dia,
Alguem poderia me dizer por que o meu pacote \usepackage[latin1]{inputenc} não está funcionando?
glp40hs talvez vc precise usar \usepackage[utf-8]{inputenc} pois por exemplo no MAC que praticamente todos os editores são utf-8 usar o latin1 causa um sumiço nos acentos. Pode ser seu caso, verifique se o editor que você está usando grava em uft-8 ou iso-8859-1
Patrocínio
Destaques
Artigos
Papagaiando o XFCE com temas e recursos
WhatsApp com Chamadas no Linux via Waydroid
XFCE - quase um Gnome ou Plasma mas muito mais leve
LXQT - funcional para máquinas pererecas e usuários menos exigentes
Dicas
Manutenção básica para Gentoo Linux (com script)
Conheça o Zashterminal, um terminal moderno com IA
DOOM Carniceiro: rode o Meatgrinder com uzdoom (Gentoo e Ubuntu)
Samba 4 AD-DC 2026: Como instalar e configurar um Active Directory (via APT-GET)
[Resolvido] Sumiço de redes e micro quedas no iwd/iwgtk (Realtek rtw88)
Tópicos
eu queria saber no lenovo slim, se tem como ver os mhz de memoria e tu... (3)
Top 10 do mês
-

Xerxes
1° lugar - 116.089 pts -

Fábio Berbert de Paula
2° lugar - 54.796 pts -

Buckminster
3° lugar - 25.469 pts -

Mauricio Ferrari (LinuxProativo)
4° lugar - 18.019 pts -

Sidnei Serra
5° lugar - 17.597 pts -

Alberto Federman Neto.
6° lugar - 17.341 pts -

Alessandro de Oliveira Faria (A.K.A. CABELO)
7° lugar - 16.923 pts -

Daniel Lara Souza
8° lugar - 16.851 pts -

edps
9° lugar - 16.401 pts -

Andre (pinduvoz)
10° lugar - 15.132 pts