Algoritmos de compressão
Este artigo faz uma apresentação dos algoritmos de compressão e qual a lógica de funcionamento dos mesmos. É o primeiro de uma série de três artigos que pretendo escrever falando sobre isso, que serão divididos em como começou, o que usamos hoje em dia, e por último a prática com implementação dos mais usados.
[ Hits: 12.814 ]
Por: Pablo Margreff em 23/03/2016 | Blog: https://pmargreff.wordpress.com/
Árvores de Huffmann
O funcionamento das árvores de Huffman são ao mesmo tempo simples e eficiente. A ideia do algoritmo é quanto menos vezes um símbolo aparece, mais distante ele irá ficar da raiz da árvore, e logicamente quanto mais vezes ele aparece, mais próximo ele estará perto da raiz.
Outro passo essencial para que a árvore possa se bifurcar quando necessário é que todo símbolo seja uma folha, e nunca um nodo da árvore. Vamos começar com a cadeia de caracteres "AACBAAABAC". O Primeiro passo é, conferir o número de vezes que cada símbolo aparece. Nesse caso: A -> 6 , B & C -> 2.
Sabendo disso, já temos que a letra que irá ficar mais próxima da raiz. Como temos apenas três letras fica fácil de montar a árvore. Nos exemplos, irei representar no nodo o número de caracteres restante, mais para ficar mais claro podemos usar os símbolos que estão a partir daquele ramo.


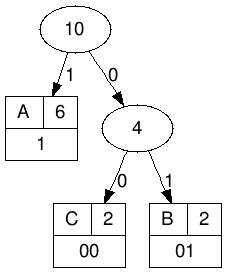
Fontes:
2. Códigos de comprimento variável
3. Árvores de Huffmann
4. Classe Lempel-Ziv-Welch
5. Conclusões
Aumentando sua produtividade com o teclado padrão Dvorak
Manipulação de imagens no formato PPM
Compilando o kernel no Conectiva Linux 10
Compilando ou atualizando um kernel Linux
Debian Linux: Atualizando o kernel 2.6.24 para 2.6.26.3 (versão estável)
Como compilar o kernel do Linux (testado e revisado)
Slamd64: O Slackware para 64 bits
Patrocínio
Destaques
Artigos
Gentoo binário em 2026: UEFI, LUKS, Btrfs e Systemd
Trabalhando Nativamente com Logs no Linux
Jogando Daikatana (Steam) com Patch 1.3 via Luxtorpeda no Linux
LazyDocker – Interface de Usuário em Tempo Real para o Docker
Dicas
Por que sua empresa precisa de uma PKI (e como automatizar EMISSÕES de certificados via Web API)
Instalando NoMachine no Gentoo com Systemd (acesso Remoto em LAN)
Gentoo: Trocando wpa_supplicant pelo iwd no NetworkManager (Systemd)
OCS Inventory NG: Instalação de Agentes Linux e Windows + Autenticação HTTP
Tópicos
O Free Download Manager não abre no Fedora 43 KDE Plasma (2)
O que houve com slackware ??? (9)
Permissão acesso as pastas servidor Ubuntu Server 24.04 (5)
Top 10 do mês
-

Xerxes
1° lugar - 125.377 pts -

Fábio Berbert de Paula
2° lugar - 59.552 pts -

Buckminster
3° lugar - 30.561 pts -

Alessandro de Oliveira Faria (A.K.A. CABELO)
4° lugar - 19.992 pts -

Alberto Federman Neto.
5° lugar - 19.653 pts -

Mauricio Ferrari (LinuxProativo)
6° lugar - 19.156 pts -

edps
7° lugar - 17.837 pts -

Daniel Lara Souza
8° lugar - 17.256 pts -

Diego Mendes Rodrigues
9° lugar - 17.086 pts -

Andre (pinduvoz)
10° lugar - 15.383 pts





